迈向自动化的第一步——

0x00 基本模型

概述
1
2
3
4
5
6
1 void sum(a,b){
2 int x = a;
3 int y = b;
4 int z = x + y;
5 return z;
6 }
调用\(sum(1,2)\)，学过C语言的都知道会发生什么事情
但如果我调用\(sum(a1,a2)\)，并且我在这之前并未声明a1，a2呢？
先不要用C语言的思路来考虑了，我们称这种情况为符号执行(Symbolic Execution)，具体会发生什么我们接着往下看
基本思想
1. 使用符号变量代替具体值作为程序或函数的参数，并模拟执行程序中的指令，各指令的操作都基于符号变量进行，其中操作数的值由符号和常量组成的表达式来表示
  1. 符号变量是什么？
    1. 读者可以将符号执行视为程序具体执行的自然扩展，符号变量使得程序执行变得不确定，当我们给一系列符号赋一个确定的值时，符号执行就成为了程序具体执行（i.e. 程序的一次具体执行可以视为符号执行的一次实例）
  2. 操作数是什么？
2. 对于任意程序，其执行流程是由执行序列的执行语义控制的
  1. 执行语义：
    1. 变量定义语句对数据对象的描述 int a;
    2. 声明语句对程序数据对象的修改 a = 10;
    3. 条件语句对程序执行流程的控制
3. 当程序的输入参数确定时，其指令序列被固定，因此程序执行语义和控制流也被固定
程序语言定义
1. James C. King在提出符号执行技术的同时，也为其限定了理想的适用场景：
  1. 理想模型中程序只处理“有符号整数”
  2. 程序“执行数”规模有限
  3. 可以处理程序内所有if条件语句的约束表达式
2. 基于符号执行技术的理想场景，对程序语言做如下定义
  1. 程序变量类型：只包含“有符号整数”
  2. 程序语句类型
    1. 简单声明语句，如a = 3
    2. if条件语句(包括then 和 else)
    3. 无条件跳转语句，如goto语句
    4. 变量操作语句：如read函数、基本整数运算操作（+、-、*）
  3. 程序语义
    1. 简单声明语句、无条件跳转语句和变量操作语句，只是将程序中的具体值替换为了符号
    2. 而if条件语句中，将具体值替换为了符号，所以我们无法判断if语句中的真值，就不能确定条件分支的走向，这是符号执行技术对程序执行语义的最大改变，也是符号执行与具体执行的关键区别
程序执行状态
- PC
  1. 为了解决“分支走向不确定”的问题，King为程序状态新添加了一个变量：路径约束条件 pc(path constraint)，在每个if条件语句处并没有实际决定程序执行哪个分支，这就需要符号执行引擎主动选择执行分支并记录整个执行过程，pc就辅助完成了这项工作
  2. Simply，pc就是符号执行过程中对路径上条件分支走向的选择情况
  3. 来看一段示例
    1
    2
    3
    if1: a1 >= 0
    if2: a1+2*a2 >= 0
    if3: a3>= 0
  4. 假设上述三个分支中选择了if1:true if2:true if3:false，pc表示为pc = (a1 >= 0 && a1+2*a2 >= 0 && ~(a3 >= 0))，由此可见，pc是一个bool表达式
- 符号执行引擎
  - 当符号执行到 if(q) 时，pc 有可能包含q（1），也可能包含 ~q（2），如果符号执行引擎选择进入then分支，则 pc 表现为（1）的形式，如果符号执行引擎选择进入else分支，则 pc 表现为（2）的形式
  - 而我们希望两条分支都被测试，所以符号执行引擎执行到if条件语句时，符号执行需要创建两个“并行”的执行过程
  - 每个和符号变量相关的if条件语句都会为pc贡献一个决定程序执行走向的表达式，最后要确定pc对应路径的程序输入参数，只需要用约束求解器对pc进行求解
符号执行树
1. 定义：用来描述程序执行路径的树形结构
2. 内容：一个节点对应程序中的一条语句，还可以包含指令计数、PC、变量值等程序执行状态信息(没找到合适的图，就先放一张不带C代码的)
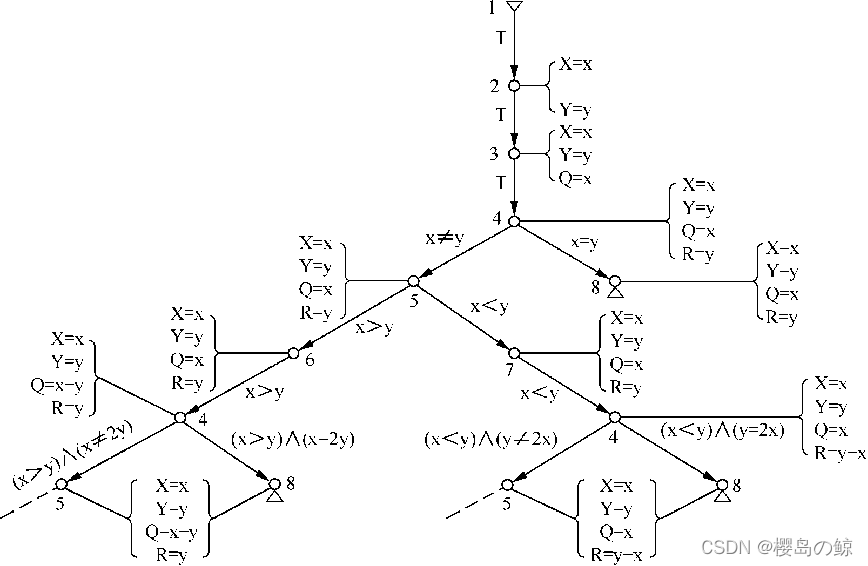
约束求解
1. 定义：
  1. 给定一个三元组<V,D,C>,其中：
    1. V: 变量的有限集合
    2. D: 变量的论域，变量可能取值的有限集合
    3. C: 有限约束集合，某个约束关系\(C_i\)包含V中一个或多个变量，若\(C_i\)包含k个变量，则称其为在这k个变量集合上的k元约束
  2. 约束求解就是找到约束问题的一个解，该解对变量集合中所有变量都赋一个取自其论域的值，并且这些变量的值满足该问题的所有约束条件
  3. 对于约束问题\(P = <V,D,C>\)，若P至少存在一个解，则称P为可满足的，否则称其为不可满足的
2. 分类:
  1. SAT(The Satisfiability problem, 可满足性问题)
    1. 定义：求解由布尔变量集合所构成的布尔函数，是否存在变量的一种分布使得该函数的取值为1
    2. 缺陷：①只能解决命题逻辑公式问题，很多实际问题转化不成命题逻辑问题②必须用布尔变量来表示，将实际问题转化为布尔函数开销大，转换后的函数也极其复杂
  2. SMT(Satisfiability Modulo Theories, 可满足性模理论)
    1. 定义：将SAT只能求解命题逻辑公式问题扩展为可以解决一阶逻辑所表达的公式。包含多种理论。
      1. 什么是一阶逻辑
回到开始的函数

1  void sum(a,b){
2    int x = a;
3    int y = b;
4    int z = x + y;
5    return z;
6  }

我们将其写为类PL/1语言

1  SUM: PROCEDURE(A,B);
2    X<-A;
3    Y<-B;
4    Z<-X+Y;
5    RETURN(Z);
6  END;

我们在调用\(sum(1,2)\)后，可以列一个表格来观察程序流
\[ \def\arraystretch{.7} \begin{array}{|c|c|c|c|c|c|c|} \hline Line & X & Y & Z & A & B & pc \cr \hline 1 & ? & ? & ? & 1 & 2 & true \cr \hline 2 & 1 & ? & ? & 1 & 2 & true \cr \hline 3 & 1 & 2 & ? & 1 & 2 & true \cr \hline 4 & 1 & 2 & 3 & 1 & 2 & true \cr \hline \end{array} \] > Line 5是return 3 (Katex不支持合并单元格，理解万岁)

我们在调用\(sum(a1,a2)\)后，就是把具体值换成了对应的符号 \[ \def\arraystretch{.7} \begin{array}{|c|c|c|c|c|c|c|} \hline Line & X & Y & Z & A & B & pc \cr \hline 1 & ? & ? & ? & a1 & a2 & true \cr \hline 2 & a1 & ? & ? & a1 & a2 & true \cr \hline 3 & a1 & a2 & ? & a1 & a2 & true \cr \hline 4 & a1 & a2 & a3 & a1 & a2 & true \cr \hline \end{array} \]

Line 5是return (a1+a2)

既然符号执行与具体值执行最大的区别是if条件语句，那么我们写一个带有if语句的程序来看一下

 1: POWER: PROCEDURE(X, Y);
 2:     Z = 1;
 3:     J = 1;
 4:
 5: LAB: IF Y >= J THEN
 6:         DO;
 7:             Z = Z * X;
 8:             J = J + 1;
 9:             GO TO LAB;
10:         END;
11:
12:     RETURN(Z);
13: END POWER;

这个函数转化为C就是

int power(int X, int Y) {
    int Z = 1;
    int J = 1;
    while (Y >= J) {
        Z *= X;
        J++;
    }
    return Z;
}

我们继续用表格的格式来看

\[ \def\arraystretch{.6} \begin{array}{|c|c|c|c|c|c|} \hline Line & Z & J & X & Y & pc \cr \hline 1 & ? & ? & a1 & a2 & true \cr \hline 2 & 1 & ? & a1 & a2 & true \cr \hline 3 & 1 & 1 & a1 & a2 & true \cr \hline \end{array} \]

前三行都很正常，直到第五行进行判断
1. 处理判断语句 Y>=J 得到约束条件 a2>=1 2. 生成两个分支的路径约束条件：
- (a2>=1) \(\subset\) true - ~(a2>=1) \(\subset\) true 3. 两个路径约束都可满足，分别对两个路径进行探索

对于分支: ~(a2>=1) \(\subset\) true

\[ \def\arraystretch{.6} \begin{array}{|c|c|c|c|c|c|} \hline Line & Z & J & X & Y & pc \cr \hline 5 & 1 & 1 & a1 & a2 & ~(a2>=1) \cr \hline \end{array} \]

然后马上在Line 12处得到(return 1 when a2<1)，探索完成

对于分支: (a2>=1) \(\subset\) true

\[ \def\arraystretch{.6} \begin{array}{|c|c|c|c|c|c|} \hline Line & Z & J & X & Y & pc \cr \hline 5 & 1 & 1 & a1 & a2 & (a2>=1) \cr \hline 7 & a1 & 1 & a1 & a2 & (a2>=1) \cr \hline 8 & a1 & 2 & a1 & a2 & (a2>=1) \cr \hline \end{array} \]

然后因为Line 9，程序会跳回第四行继续判断语句，会产生两个新的分支，就陷入了无限循环，这不是我们想要的。

可是循环在一个程序中经常出现，该怎么解决这一问题？我们接着往后看

0x01 动态符号执行技术(DSE)

基本思想
1. 以具体的数值作为输入，执行程序代码，在程序实际执行路径的基础上：
  1. 用符号执行技术对路径进行分析
  2. 提取路径的约束表达式
  3. 根据路径搜索策略(深度、广度)对约束表达式进行变形
  4. 求解变形后的表达式并生成新的测试用例
  5. 不断迭代上述过程，直到完全遍历程序的所有执行路径
2. DSE的出现是为了解决静态SE①执行效率低②系统开销大③误报率高的问题
实现细节(以函数为例)
1. 场景：void func(int a,int b),调用func(X,Y)
2. Step1: 生成一组随机输入，开始"实际执行"
3. Step2: 同时符号引擎开始符号执行，按照“实际执行”的“执行路径”上的分支条件语句的“谓词”，搜集所有符号约束条件及其对应真值
4. Step3: 根据收集到的符号约束条件，按照一定路径选择策略，构造出一条新的可行路径约束
  - 举个例子：深度优先策略
  - 如果pc = p1 ∩ p2 ∩ p3, 深度优先就是将最后一个谓词(对不起jo太郎😭离散没学好忘了这个p3叫啥了)取非，变为p1 ∩ p2 ∩ ~p3
5. Step4: 使用约束求解器求解出新约束集合对应的具体输入
6. Step5: 重复上述过程，直到遍历全部路径
DSE工具SAGE
1. 原理粗略地过了一遍，大段大段的看不懂😭这里就不花时间总结了
2. SAGE基于x86的机器码进行符号执行，原因如下：
  1. 屏蔽不同编程语言、编译器及编译平台对分析过程的影响，具有更强的复用性
  2. 忽略编译器"代码优化""代码混淆""基本块转换"等使代码语义发生变化的操作，有利于确定程序实际存在的漏洞
  3. 闭源分析yyds
关键问题
1. 外部函数调用
2. 循环问题：路径爆炸

这一段也不仔细读了...用到再学

0x02 并行符号执行技术(PSE)

基本思想
1. 很多情况下符号执行引擎无法继续运行的原因是内存不足，所以我们希望通过计算集群可无穷扩展的内存空间和CPU来缓解路径爆炸问题
2. 分布式...这我就先不看了

0x03 参考文献

1《软件安全分析与应用》

HeyGap's_Blog

Symbolic Execution Leaning Note (1) -- Basis

0x00 基本模型

0x01 动态符号执行技术(DSE)

0x02 并行符号执行技术(PSE)

0x03 参考文献